في عهد المأمون (813-833) ، والدولة العباسية في ذروتها. طلب الخليفة من الخوارزمي ، وهو عالم مشهور عمل في بيت الحكمة في بغداد، تقييم الطرق الرياضية المفيدة في إدارة هذه الدولة الضخمة التي تمتد من آسيا الوسطى إلى جبال البرانس
في هذه ألأطروحة، الخوارزمي هو أول من درس دراسة منهجية لمجموعة من المعادلات.
وتغطي هذه الدراسة الحلول الكاملة معادلة رياضية من الدرجة الأولى والثانية، والتي يمكن كتابتها بالشكل الحديث
مع 
، 
و
ثلاثة أعداد، مع الذي يمكن أن يكون معدوم. ويعتبر الخورزمي ثلاثة أنواع من الأعداد : الأعداد (التي ندعوما ثوابت نرمز لها أعلاه بـ ) التي يدعوها باسم العملة درهم ، الجذور (الحلول، جذر الكلمة بمعنى "ما هو خفي "ويحتاج إلى استخراج، ونرمز له بـ
)، و مربع الجذر (بالتالي 
). يتضمن هذا المقال الكتابة الحديثة لتسهيل المتابعة للقارئ المعاصر، هذا أن كتاب المختصر في في حساب الجبر والمقابلة ، لم يحتوي على مثل هذا النوع من الكتابة (والتي لم يكن معمولا بها)، حيث أن جميع العمليات تم وصفها عن طريق الجمل.
، و ثلاثة أعداد، مع الذي يمكن أن يكون معدوم. ويعتبر الخورزمي ثلاثة أنواع من الأعداد : الأعداد (التي ندعوما ثوابت نرمز لها أعلاه بـ ) التي يدعوها باسم العملة درهم ، الجذور (الحلول، جذر الكلمة بمعنى "ما هو خفي "ويحتاج إلى استخراج، ونرمز له بـ)، و مربع الجذر (بالتالي ). يتضمن هذا المقال الكتابة الحديثة لتسهيل المتابعة للقارئ المعاصر، هذا أن كتاب المختصر في في حساب الجبر والمقابلة ، لم يحتوي على مثل هذا النوع من الكتابة (والتي لم يكن معمولا بها)، حيث أن جميع العمليات تم وصفها عن طريق الجمل.
لكن، في ذلك الوقت لم يكن يعرف علماء الرياضيات الأرقام السالبة مما أدى به إلى التمييز بين ستة حالات التي تكون فيها الأعداد ، و كلها موجبة :
، و كلها موجبة :- المربعات تساوي الجذور :
؛ - المربعات تساوي الأعداد :
؛ - الجذور تساوي الأعداد :
؛ - المربعات والجذور تساوي الأعداد :
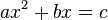؛ - المربعات والأعداد تساوي الجذور :
؛ - الجذور والأعداد تساوي المربعات :
.
أي معادلة من الدرجة الأولى أو الثانية يمكن تحويلها إلى إحدى الحالات الست المذكورة أعلاه بمعاملات موجبة. لهذا، استخدم الخوارزمي التقنيتين التي أعطت اسمها للكتاب : الجبر والمقابلة هما جانبان مما يصطلح به اليوم بالتحويل
الجبر
الجبر بمعنى "جبر الكسر" ،حيث تم نقل الكلمة إلى اللاتينية، وأصبحت algebra. ' الجبر هو تبسيط المعادلة من خلال إزاله الطرح وهذا بإضافة حدود في طرفيها. أي بالمصطلح الحديث الحصول على معادلة بمعاملات موجبة.
مثال :
x2 = 40x − 4x2 تحول بالجبر إلى x2 + 4x2 = 40x, ثم إلى 5x2 = 40x.
في الواقع، الخوارزمي، حيث يعين تطرح شركة (مثل 2 × 4 في المثال السابق) : nâqis "التهرب". الكلمة المستخدمة هي نفسها للدلالة على أطرافه لمبتوري الأطراف . آل جبر وبالتالي لاستعادة ما هو مفقود في المعادلة.
المقابلة
إزالة الطرح بالجبر ليس كافيا للحصول على إحدى الحالات الست.
x2 on soustrait x2 pour obtenir 5 = 40x + 3x2.
ليست هناك تعليقات:
إرسال تعليق